Floyd-Warshall algoritms

Ja līdz šim tika apskatīti algoritmi, kā aprēķināt īsāko ceļu no vienas virsotnes līdz pārējām, tad tagad varētu apskatīt, kā aprēķināt efektīvi īsāko ceļu starp jebkurām divām virsotnēm.

Variants ir izmantot Deikstras vai Belmana-Forda algoritmu, bet tas var nebūt pārāk efektīvi. Tādēļ variants ir izmantot DP algoritmu, kuru var uzrakstīt dažās rindās.

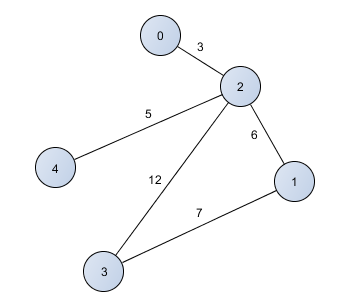
Sākotnēji ir nepieciešams izveidot grafa kaimiņu matricu. Kaimiņu matricā M elements M[i][j] satur svaru, ja šķautne ar šo svaru savieno virsotnes i un j. DP algoritmā M[i][j] satur ceļa garumu, ja no i uz j eksistē ceļš. Piemēram, vienas komponentes neorientētā grafā ceļš eksistē no jebkuras uz jebkuru virsotni. DP ideja ir, ka DP[i][j] = minimālā vērtība DP[i][k] + DP[k][j]. Tātad apskatot visas k vērtības, ir iespējams atrast minimālo DP[i][k] + DP[k][j]. Programmas paraugs ir apskatāms 1. programmā. Grafs, kuram tiek veidota programma, ir apskatāms 1. attēlā.

#include <iostream>

#include <cstdio>

#include <vector>

#define SIZE 5

#define INF 200000000

using namespace std;



int dp[SIZE][SIZE] = {

    {INF, INF, 3, INF, INF},

    {INF, INF, 6, 7, INF},

    {3, 6, INF, 12, 5},

    {INF, 7, 12, INF, INF},

    {INF, INF, 5, INF, INF}

};



void floyd_warshall(int n)

{

    for (int i = 0; i < n; ++i)

        for (int j = 0; j < n; ++j)

            for (int k = 0; k < n; ++k)

                if (dp[i][j] > dp[i][k] + dp[k][j])

                {

                    dp[i][j] = dp[i][k] + dp[k][j];

                }

}



int main()

{

    floyd_warshall(SIZE);



    for (int i = 0; i < SIZE; ++i)

    {

        for (int j = 0; j < SIZE; ++j)

            cout << dp[i][j] << " ";

        cout << endl;

    }



    return 0;

}