Prima algoritms

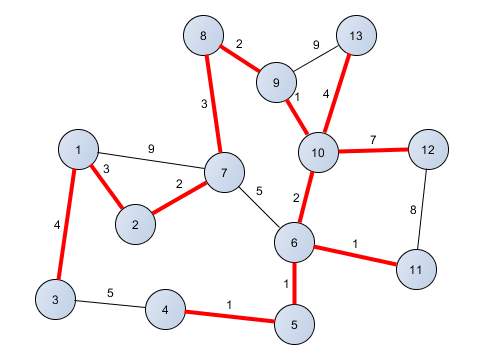
Prima algoritms minimālā pārklājošā koka atrašanai strādā sekojoši:

1. Kokā iekļauj vienu sākuma virsotni.
2. Kaudzē ieliek šķautnes, kuras ved no 1. virsotnes uz citām.
3. Kamēr kaudze nav tukša.
   1. Izņem šķautni no kaudzes.
   2. Ja pievienojamā virsotne vēl nav pievienota kokam, tad pievieno to ar šķautni.
   3. Ieliek visas pievienojamās virsotnes uz kokā neiekļautajiem kaimiņiem vedošās šķautnes.
4. Izvada rezultātā kokā iekļauto virsotņu šķautnes.

#include <iostream>

#include <algorithm>

#include <vector>

#include <queue> // priority_queue

#define SIZE 17

#define VERTEX_COUNT 13

using namespace std;



struct edge{

    int n;

    int weight;

};



struct full_edge {

    int m;

    int n;

    int weight;

};



int data[][3] = {

    { 1, 2, 3 },

    { 1, 7, 9 },

    { 1, 3, 4 },

    { 2, 7, 2 },

    { 3, 4, 5 },

    { 4, 5, 1 },

    { 5, 6, 1 },

    { 6, 7, 5 },

    { 6, 11, 1 },

    { 11, 12, 8 },

    { 10, 12, 7 },

    { 6, 10, 2 },

    { 10, 13, 4 },

    { 10, 9, 1 },

    { 9, 13, 9 },

    { 8, 9, 2 },

    { 8, 7, 3 },

};



vector<edge> v[VERTEX_COUNT + 1];



// Klase ir jāinicializē, lai varētu queue pateikt, kā salīdzināt divus struktūras tipa mainīgos.

class cmp

{

public:



    bool operator() (const full_edge &a, const full_edge &b) const

    {

        return a.weight > b.weight;

    }

};



void prim(int u, vector<full_edge> &edges)

{

    // Heap prioritātes rinda. O(log(N)) meklēšana, ievietošana, izmešana.

    priority_queue<full_edge, vector<full_edge>, cmp> q;

    bool *node_taken = new bool[VERTEX_COUNT + 1];



    // Ieliek sākotnējās šķautnes.

    for (int i = 0; i < v[u].size(); ++i)

    {

        full_edge tmp;

        tmp.n = v[u][i].n;

        tmp.weight = v[u][i].weight;

        tmp.m = u;

        q.push(tmp);

    }

    node_taken[u] = true;



    while (!q.empty())

    {

        full_edge u = q.top();

        q.pop();

        if (!node_taken[u.n])

        {

            edges.push_back(u);

            node_taken[u.n] = true;

            for (int i = 0; i < v[u.n].size(); ++i)

                if (!node_taken[v[u.n][i].n])

                {

                    full_edge tmp;

                    tmp.n = v[u.n][i].n;

                    tmp.weight = v[u.n][i].weight;

                    tmp.m = u.n;

                    q.push(tmp);

                }

        }

    }

}



int main()

{

    // Ieliekam datus struktūras objektos.

    // Šeit varētu būt arī datu ielasīšana.

    for (int i = 0; i < SIZE; ++i)

    {

        edge e;

        e.n = data[i][1];

        e.weight = data[i][2];

        v[data[i][0]].push_back(e);



        e.n = data[i][0];

        v[data[i][1]].push_back(e);

    }



    vector<full_edge> edges;

    prim(1, edges);



    // Izvadām rezultātus.

    for (int i = 0; i < edges.size(); ++i)

        cout << edges[i].m << " " << edges[i].n << " " << edges[i].weight << endl;



    return 0;

}