Kruskāla algoritms
Minimālai pārklājošais koks ir tāda neorientēta svērta grafa šķautņu kopa, kas veido koku, aptver visas virsotnes un kuras šķautņu svaru summa ir minimālā iespējamā. Maksimālais pārklājošais koks ir tas pats minimālais pārklājošais koks, tikai ar maksimālo iespējamo šķautņu svaru summu. Piemēru var apskatīt 1. attēlā, kā arī veidu, kā aprēķināt šāda grafa minimālo pārklājošo koku var redzēt 1. programmā.
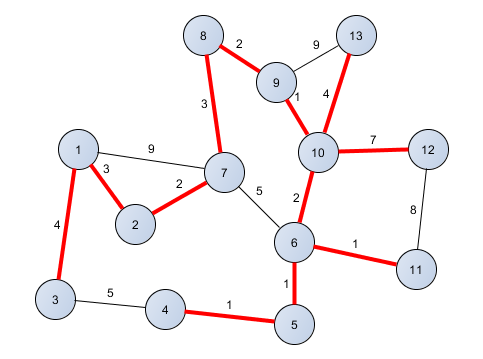
Kruskāla algoritms minimālā pārklājošā koka atrašanai strādā sekojoši:
- Saliek visas šķautnes masīvā M.
- Sakārto M pēc šķautņu svara.
- Iet cauri katrai šķautnei secīgi un skatās, ja katra virsotne galā atrodas savā komponentē (neeksistē līdz šim izveidotajā grafā cits ceļš starp abām virsotnēm), tad šķautni var pievienot veidojamajam kokam. Šajā pārbaudē var izmantot nesaistītās kopas.
- Kad N - 1 šķautnes ir izvēlētas, beidz darbu (N - virsotņu skaits).
#include <iostream>
#include <algorithm>
#include <vector>
#define SIZE 17
#define VERTEX_COUNT 13
using namespace std;
struct edge{
int n, m;
int weight;
};
int data[][3] = {
{ 1, 2, 3 },
{ 1, 7, 9 },
{ 1, 3, 4 },
{ 2, 7, 2 },
{ 3, 4, 5 },
{ 4, 5, 1 },
{ 5, 6, 1 },
{ 6, 7, 5 },
{ 6, 11, 1 },
{ 11, 12, 8 },
{ 10, 12, 7 },
{ 6, 10, 2 },
{ 10, 13, 4 },
{ 10, 9, 1 },
{ 9, 13, 9 },
{ 8, 9, 2 },
{ 8, 7, 3 },
};
vector<edge> v;
// Funkcija, lai sakārtot šķautnes pēc svara.
bool cmp(const edge &a, const edge &b)
{
return a.weight < b.weight;
}
// Nesaistīto kopu struktūra un funkcijas.
int parent[VERTEX_COUNT + 1];
int rank[VERTEX_COUNT + 1];
void make_set(int i)
{
parent[i] = -1;
rank[i] = 1;
}
int find(int i)
{
if (parent[i] == -1)
return i;
else
return find(parent[i]);
}
void unite(int a, int b)
{
a = find(a);
b = find(b);
if (rank[a] > rank[b])
{
parent[b] = a;
rank[a] += rank[b];
}
else
{
parent[a] = b;
rank[b] += rank[a];
}
}
void kruskal(vector<edge> &edges)
{
edges.clear();
sort(v.begin(), v.end(), cmp);
// Izveido nesaistītās kopas.
for (int i = 1; i <= VERTEX_COUNT; ++i)
make_set(i);
// Kokā ir VERTEX_COUNT - 1 šķautnes.
for (int i = 0; edges.size() < VERTEX_COUNT - 1; ++i)
{
// Ar nesaistīto kopu palīdzību seko līdzi, vai virsotnes neatrodas vienā komponentē.
if (find(v[i].m) != find(v[i].n))
{
unite(v[i].m, v[i].n);
edges.push_back(v[i]);
}
}
}
int main()
{
// Ieliekam datus struktūras objektos.
// Šeit varētu būt arī datu ielasīšana.
for (int i = 0; i < SIZE; ++i)
{
edge e;
e.m = data[i][0];
e.n = data[i][1];
e.weight = data[i][2];
v.push_back(e);
}
vector<edge> edges;
kruskal(edges);
// Izvadām rezultātus.
for (int i = 0; i < edges.size(); ++i)
cout << edges[i].m << " " << edges[i].n << " " << edges[i].weight << endl;
return 0;
}








