Grafu reprezentējošas datu struktūras

Grafu daudz izmanto programmēšanā. Šajā nodaļā tiks apskatīti veidi, kā glabāt grafus programmā. Īsumā tiks apskatītas masīvu un vektoru datu struktūras priekš grafiem. Eksistē arī cita veida struktūras, piemēram balstītas uz no norādēm, bet tieši šīs retāk tiek izmantotas sacensību laikā un parasti eksistē alternatīvs variants, kā vienkāršāk risināt grafu problēmu.

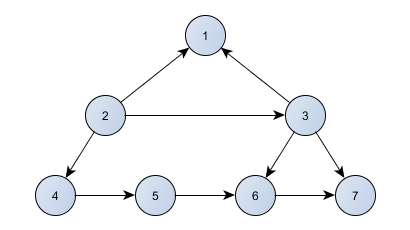
1. attēls - orientēts grafs.

Šķautņu saraksts

Vienkāršākā no šeit esošajām datu struktūrām, bet vienlīdz noderīga, piemēram Kruskala algoritmā. Ideja ir tāda, ka masīvā tiek glabātas šķautnes. Katrai šķautnei tiek glabātas tās virsotnes katrā galā. Orientēta grafa gadījumā virsotņu secībai ir nozīme. Ja grafs ir svērts, var rasties vajadzība glabāt arī šķautnes svaru. Iespējams ir citi parametri, kurus vajag glabāt. Piemēram, 1. attēlā redzamajam grafam kods varētu izskatīties sekojošs:

#include <iostream>

#include <vector>

using namespace std;



struct edge

{

    int out, in;

};



int main()

{

    vector<edge> v;

    edge e;



    e.out = 2; e.in = 1; v.push_back(e);

    e.out = 3; e.in = 1; v.push_back(e);

    e.out = 2; e.in = 3; v.push_back(e);

    e.out = 2; e.in = 4; v.push_back(e);

    e.out = 3; e.in = 6; v.push_back(e);

    e.out = 3; e.in = 7; v.push_back(e);

    e.out = 4; e.in = 5; v.push_back(e);

    e.out = 5; e.in = 6; v.push_back(e);

    e.out = 6; e.in = 7; v.push_back(e);



    for (int i = 0; i < v.size(); ++i)

        cout << v[i].out << " " << v[i].in << endl;



    return 0;

}

1. programma - šķautņu saraksta realizācija.

Kaimiņu matrica

Kaimiņu matrica ir 2 dimensiju masīvs, kur 1. dimensija nozīmē, no kuras virsotnes šķautne iet, un 2. dimensija nozīmē, uz kuru virsotni šķautne iet. Ja ir definēts mas[20][20], tas nozīmē, ka grafā ir 20 virsotnes numurētas no 0 līdz 19. Ja masīva elements ir 0, tad šķautne neeksistē, citādi šķautne eksistē starp abām virsotnēm. mas elementi var būt arī 0 vai šķautnes svars (acīm redzot svars nedrīkst būt 0). Šo datu struktūru drīkst pielāgot vajadzībām. Piemēram:

Ja grafs ir neorientēts, tad mas[i][j] == mas[j][i] jeb grafs ir simetrisks. Tas ir tādēļ, ka gan no virsotnes i var nokļūt uz virsotni j, gan otrādi.
Ja grafs ir orientēts, tad mas[i][j] ne obligāti ir mas[j][i], jo šķautne var eksistēt tikai vienā virzienā.

Piemērs 1. attēlā redzamajam grafam ir redzams 2. attēlā.

2. attēls - kaimiņu matrica.

Kaimiņu saraksts

Kaimiņu saraksts ir 1 dimensiju masīvs, kur katrs elements ir vektors. Patiesībā dēļ vektoriem, šo struktūru var izmantot, kā 2 dimensiju masīvu, viens ieguvums ir tāds, ka vektori no sākuma ir garumā 0. Kādas šai struktūrai ir privilēģijas pār kaimiņu matricu? Tādas, ka vektori palielinās dinamiski atkarībā no ielikto elementu skaita, kas ļauj matricai neaizņemt N * N (kur N ir virsotņu skaits) izmēru, bet izmēru atkarībā no šķautņu skaita. Tā kā šķautnes grafā sliktākajā gadījumā var būt N * (N - 1) / 2 jeb O(N * N), tad tikai sliktākajā gadījumā atmiņa tiks patērēta tikpat, cik kaimiņu matricā. Kaimiņu saraksts darbojas tā, ka, ja mums ir mas struktūra, tad mas[i] satur visu virsotņu numurus, uz kurām var aiziet no i virsotnes. Piemēram, 1. attēla gadījumā mas[2] satur 1, 3, 4. Programmas piemēru var apskatīt 2. programmā. Struktūras piemēru var apskatīt 3. attēlā.

#include <iostream>

#include <vector>

using namespace std;



int main()

{

    vector<int> v[8];



    v[2].push_back(1);

    v[2].push_back(3);

    v[2].push_back(4);

    v[3].push_back(1);

    v[3].push_back(6);

    v[3].push_back(7);

    v[4].push_back(5);

    v[5].push_back(6);

    v[6].push_back(7);



    for (int i = 0; i < 7; ++i)

    {

        cout << i << ": ";

        for (int j = 0; j < v[i].size(); ++j)

            cout << v[i][j] << " ";

        cout << endl;

    }



    return 0;

}

2. programma - kaimiņu saraksts.

3. attēls - kaimiņu saraksts.

Vecāku masīvs (kokiem)

Vecāku masīvs kokiem ir 1 dimensiju masīvs, kurā katrai virsotnei ir atzīmēts, kura virsotne ir tās vecāks. Piemēram, ja mas[i] == j, tas nozīmē, ka i virsotnei vecāks ir j. Acīm redzot šo struktūru var izmantot tikai kokiem, jo tikai tiem eksistē bērna-vecāka attiecība.