Binārā meklēšana

Šīs nodaļas ietvarā apskatīta tiks veselu skaitļu binārā meklēšana. Šo tehniku jeb algoritmu, kurš ir Skaldi un valdi algoritma klasisks piemērs, var izmantot arī citiem objektiem, kuriem savā starpā var noteikt secību jeb piemērot kādu no < vai > operatoriem.

Tātad problēma varētu būt sekojoša. Ir dota N = 10^6 garam skaitļu virkne un M = 1000 reizes ir jāpasaka, vai kāds skaitlis atrodas virknē. Ja laika limits ir 1 sekunde, tad acīm redzot laika limits tiks pārsniegts, jo ar rupjā spēka metode būs O(N * M) algoritms, kas būs aptuveni 10^10 iterācijas. Tiesa, izmantojot bināro meklēšanu, sarežģītība tiek samazināta uz O(log(N) * M) jeb 20000 iterācijām, kas ietilpst 1 sekundes limitā.

Binārā meklēšana strādā tā. Tiek glabātas divas vērtības up un down mainīgie, kur up sākumā ir pēdējā elementa pozīcija un down ir apakšējā elementa pozīcija. Tālāk meklējot vērtību notiek sekojošs algoritms:

1. Sakārto masīvu.
2. Kamēr up - down > 1.
3. Aprēķina mid = (up + down) / 2 pozīciju.
4. Ja meklētā vērtība >= mas[mid].
5. Tad down = mid.
6. Citādi up = mid;
7. Ja mas[down] nav vienāds ar meklēto vērtību, tad elements nav masīvā, citādi elements ir masīvā down pozīcijā.

Vizuāli tas izskatās kā 1. attēlā.

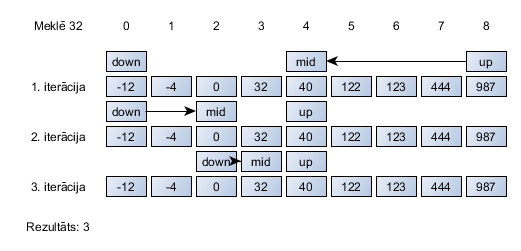
Binārās meklēšanas realizācija programmā ir apskatāma 1. programmā.

#include <iostream>

#include <algorithm>

using namespace std;



bool binara_meklesana(int mas[], int len, int val)

{

    int down = 0;

    int up = len - 1;



    while (up - down > 1)

    {

        int mid = (up + down) / 2;

        if (val >= mas[mid])

            down = mid;

        else

            up = mid;

    }



    return (mas[down] == val ? true : false);

}



int main()

{

    int mas[] = {-12, -4, 0, 32, 40, 122, 123, 444, 987};



    // Paša rakstīta funkcija.

    cout << "32 ";

    cout << (binara_meklesana(mas, 9, 32) ? "atrodas" : "neatrodas");

    cout << " masiva" << endl;



    // algorithm funkcija.

    cout << "32 ";

    cout << (binary_search(mas, mas + 9, 32) ? "atrodas" : "neatrodas");

    cout << " masiva" << endl;



    return 0;

}