Prioritāšu rinda un priority_queue<T>

Prioritāšu rindai mēdz izmantot kaudzes datu struktūru. Prioritāšu rinda patiesībā var būt plašāks jēdziens par kaudzi, jo tās mērķis ir uzturēt kārtību pēc kādas prioritātes un ļaut viegli piekļūt pēc prioritātes vis augstākajam elementam. Bet vairāk tiks apskatīta kaudzes struktūra šajā nodaļā, kā viens no veidiem, kā realizēt prioritāšu rindu.

Kaudze var būt max un min. Tas nozīmē, ka virsotnē atradīsies elements ar vis lielāko vai mazāko vērtību. Prioritāšu rindas gadījumā tiks apskatīta max kaudze, bet realizācija mainās minimāli. Kaudze ir binārs koks, kur katrā virsotnē elements ir lielāks vai vienāds, kā tās apakškoka virsotnes elementi. Koks ar šādu īpašību ir kaudze.

Pašam programmēt kaudzi var būt nedaudz sarežģīti, bet vienkāršākais variants ir to darīt ar masīva palīdzību. Ja ir doti N elementi, tad ir nepieciešams N izmēra masīvs. Pēc idejas masīva indeksi ir saistīti ar kaudzes virsotņu numerāciju (skatīt 1. attēlu).

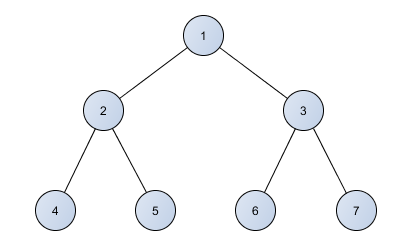
Tas nozīmē, ka masīva M[i] elements apzīmē virsotni un tā bērni ir M[2 * i] un M[2 * i + 1] elementi. Tāpat M[i / 2] ir M[i] elementa vecāks kaudzes binārajā kokā. Ņemot to vērā, kā arī atceroties kaudzes nosacījumu, sākotnēji var iziet katram elementam cauri no beigām un veikt tā "iegremdēšanu" (angliski heapify). Iegremdēšana konkrētam elementam ir rekursīva vai iteratīva funkcija, kas pārbauda, vai kāds no abiem M[i * 2] un M[i * 2 + 1] ir lielāks par M[i] (max kaudzei), ja ir, tad apmaina lielāko no bērniem ar M[i] vietām un veic šo pašu darbību ar šo bērnu (piemēram skatīt 1. programmu).

Kaudzei var veikt vairākas pamatdarbības (realizāciju skatīt 1. programmā):

• Elementa pievienošana - pieliek masīva galā elementu un "uzpeldina" to augšā. Uzpeldināšana nozīmē, ka tiek salīdzināts M[i] ar M[i / 2], ja M[i] > M[i / 2] (max kaudzē), tad apmaina abus vietām un veic uzpeldināšanu M[i / 2].
• Augšējā elementa skatīšanās - M[1] ir augšējais elements.
• Augšējā elementa izmešana - pēdējo kaudzes masīva elementu ieliek kaudzes augšā un iegremdē.

#include <iostream>

#include <vector>

#include <algorithm>

using namespace std;



// Iegremdēšana.

void heapify(int i, vector<int> &H)

{

    int nexti = i;



    while (true)

    {

        int left = i * 2;

        int right = i * 2 + 1;



        if (left < H.size() && H[i] < H[left])

            nexti = left;

        if (right < H.size() && H[nexti] < H[right])

            nexti = right;



        swap(H[i], H[nexti]);

        if (nexti != i)

            i = nexti;

        else

            break;

    }

}



// Uzpeldināšana.

void heapify_rev(int i, vector<int> &H)

{

    while (i > 1 && H[i / 2] < H[i])

    {

        swap(H[i / 2], H[i]);

        i /= 2;

    }

}



void heap_make(vector<int> &H)

{

    for (int i = H.size() - 1; i >= 0; --i)

        heapify(i, H);

}



void heap_pop(vector<int> &H)

{

    swap(H[0], H[H.size() - 1]);

    H.pop_back();

    if (!H.empty()) heapify(0, H);

}



void heap_insert(int val, vector<int> &H)

{

    H.push_back(val);

    heapify_rev(H.size() - 1, H);

}



int heap_top(vector<int> &H)

{

    return H[0];

}



int main()

{

    int N[] = {9, 1, 10, -11, 6, 4, 2};

    vector<int> H(N, N + 7);



    heap_make(H);



    heap_insert(5, H);

    heap_insert(-88, H);

    heap_insert(0, H);



    while (!H.empty())

    {

        cout << heap_top(H) << endl;

        heap_pop(H);

    }



    return 0;

}

 

STL priority_queue<T>

Prioritāšu rinda C++ ir iespējams realizēt ar priority_queue klasi queue bibliotēkā, kur ievietošanas un izmešanas no kaudzes augšas darbības ir O(log(n)), bet augšējā elementa apskatīšana notiek konstantā laikā. Piemēru, kā izmantot priority_queue , var apskatīt 2. programmā.

#include <iostream>

#include <queue>

using namespace std;



int main()

{

    int sk[] = {88, 3, 22, 7, 0, -5, -99};



    priority_queue<int> pq(sk, sk + 7);



    while (!pq.empty())

    {

        cout << pq.top() << endl;

        pq.pop();

    }



    return 0;

}