Maksimālā sapārojuma atrašana
Maksimālā sapārojuma problēma ir mēģinājums atrast tādu grafa šķautņu kopu M, kur nevienām divām šķautnēm nav kopīga virsotne. Šai problēmai ir vairāki termini:
- Maksimālais sapārojums - tāds sapārojums, kurš neļauj nevienai citai šķautnei tikt pievienotai M, lai nerastos pretruna divdaļīgā sapārojuma definīcijā.
- Maksimuma sapārojums - tāds sapārojums, kurš ir maksimālais un pie reizes iekļauj lielāko iespējamo šķautņu skaitu kopā M.
- Perfektais sapārojums - tāds maksimuma sapārojums, kurā visas virsotnes saskaras ar kādu no M kopas šķautnēm.
- Gandrīz perfekts sapārojums - perfekts sapārojums, kur tieši vienai virsotnei nepieiet neviena M šķautne klāt.
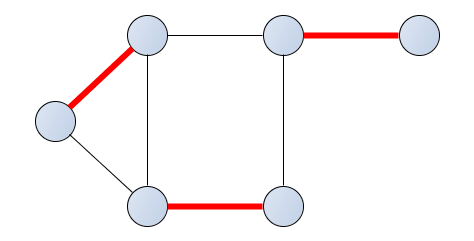
Piemērs perfektam grafa sapārojumam ir apskatāms 1. attēlā. Tālāk nodaļā tiks runāts par divdaļīga grafa sapārošanu, kas ir apakšproblēma grafa sapārošanai. Vairāk par vispārīgu grafa sapārošanu var lasīt zemāk pieejamajā informācijas saitē.
Divdaļīga grafa sapārošana
Divdaļīgs grafs - neorientēts grafs, kurā virsotnes ir sadalītas 2 apakškopās (X un Y) un kurā šķautne var eksistēt starp divām virsotnēm tikai tad, ja viena virsotne atrodas A apakškopā un otra atrodas B apakškopā.
Maksimālais sapārojums - Ir dots divdaļīgs grafs ar tā šķautnēm. Lielākā iespējamā šķautņu apakškopa, kur neviena virsotne nav savienota ar vairāk kā vienu citu virsotni.
Piemērs bildē:

Maksimālā sapārojuma problēmu var risināt ar Ford-Fulkerson algoritmu (risina maksimālo plūsmu problēmu), modificējot doto grafu:
Dotais grafs tiek transformēts uz orientētu grafu - visas šķautnes iet virzienā no X kopas virsotnes uz Y kopas virsotni.
Grafam tiek pievienotas 2 virsotnes s un t.
Tiek pievienotas šķautnes no t uz visām X kopas virsotnēm.
Tiek pievienotas šķautnes no visām Y kopas virsotnēm uz virsotni t.
Visām šķautnēm tiek piešķirta kapacitāte 1.
Piemērs bildē:

Maksimālā plūsma no s uz t būs maksimālā sapārojuma šķautņu skaits. Un šķautnes, kuras iet no kopas X uz kopu Y un kurās plūsma ir 1, ir maksimālā sapārojuma šķautnes.








