Sapārojuma pārbaude

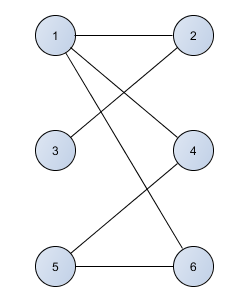
Divdaļīgs grafs ir tāds, kura virsotnes var sadalīt tādās divās netukšās kopās, kur katrā kopā starp kopas virsotnēm neeksistē šķautnes (skatīt 1. attēlu).

Lai pārbaudītu, vai grafs ir divdaļīgs, ir jāmēģina grafu nokrāsot ar 2 krāsām, ja to neizdodas izdarīt, tad grafs nav divdaļīgs.

#include <iostream>

#include <vector>

using namespace std;



vector<int> v[7];

int color[7];



bool check_bipartite(int node, int c = 1)

{

    bool ans = true;

    color[node] = c;

    for (int i = 0; i < v[node].size() && ans; ++i)

    {

        if (!color[v[node][i]])

            ans = ans && check_bipartite(v[node][i], c % 2 + 1);

        if (ans && color[v[node][i]] == c) {

            ans = false;

        }

    }



    return ans;

}



int main()

{

    v[1].push_back(2);

    v[1].push_back(4);

    v[1].push_back(6);

    v[2].push_back(1);

    v[2].push_back(3);

    v[3].push_back(2);

    v[5].push_back(4);

    v[5].push_back(6);

    v[4].push_back(5);

    v[4].push_back(1);

    v[6].push_back(1);

    v[6].push_back(5);



    cout << (check_bipartite(1) ? "Ir divdaligs." : "Nav divdaligs.") << endl;



    return 0;

}