Meklēšana dziļumā

Meklēšana dziļumā jeb DFS (Depth First Search) tā tiek saukta dēļ tā, kā norit grafa apstaigāšana. Parasti apstaigāšana tiek sākta ar vienu virsotni. Tālāk tiek izvēlēta kāda no neapmeklētajām kaimiņu virsotnēm. Kad algoritms ir aizgājis līdz virsotnei, kurai vairs nav neapmeklētu kaimiņu, tā ir nokļuvusi tik dziļi, cik tas ir iespējams un notiek kāpšanās atapakaļ.

Šādu uzvedību var iegūt izmantojot rekursiju. Meklēšana dziļumā ir klasisks rekursīvs algoritms. Tieši grafa apstaigāšanai ir nepieciešams zināt par virsotni, vai tā ir apmeklēta, vai nē. Tādēļ virsotnes tiek numurētas no 0 līdz N - 1 un to stāvoklis atzīmēts masīvā visited[i].

Šī algoritma sarežģītība ir ļoti atkarīga no datu glabāšanas veida. Ja dati tiek glabāti kaimiņu sarakstā, sarežģītība ir O(V + E). Ja dati tiek glabāti kaimiņu matricā, sarežģītība ir O(V^2). E - šķautņu skaits. V - virsotņu skaits.

#include <iostream>

#include <cmath>

#include <vector>

#include <string.h>

using namespace std;



vector<int> v[7];

// Šo masīvu izmanto, lai rekursija nesāktu riņķot uz riņķi.

// Masīvā atzīmē apmeklētās virsotnes.

bool visited[7];



void dfs(int node)

{

    visited[node] = true;

    cout << node << endl;

    for (int i = 0; i < v[node].size(); ++i)

        if (!visited[v[node][i]])

        {

            dfs(v[node][i]);

        }

}



int main()

{

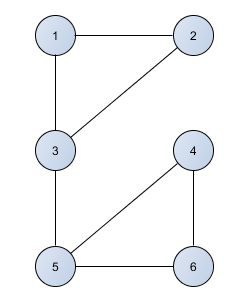
    v[1].push_back(2);

    v[1].push_back(3);

    v[2].push_back(1);

    v[2].push_back(3);

    v[3].push_back(1);

    v[3].push_back(2);

    v[3].push_back(5);

    v[5].push_back(3);

    v[5].push_back(4);

    v[5].push_back(6);

    v[4].push_back(5);

    v[4].push_back(6);

    v[6].push_back(4);

    v[6].push_back(5);



    dfs(1);



    return 0;

}

 

Rekursijas izsekošana

Ir reizes, kad ir nepieciešams uzzināt, kādā secībā rekursija apmeklēja virsotnes, lai nokļūtu no virsotnes u uz v. Varētu teikt, ka ir jāuzzina ceļš (u, v), kuru noiet meklēšana dziļumā. To var uzzināt ieviešot masīvu backtrack[i], kur i ir virsotne un backtrack[i] ir virsotne, no kuras tika veikts ceļš uz i. Ja ir nepieciešams uzzināt ceļu (u, v), tad var ieviest rekursiju dfsPrintPath(v):

// Šī ir funkcija, kuru jāizmanto kopā ar kādu papildus algoritmu,

// kurš uzģenerē backtrack[i] masīvu.

int backtrack[7], u, v;



void dfsPrintPath(int i){

    cout << i << " ";

    if (backtrack[i] >= 0 && i != u) {

        dfsPrintPath(backtrack[i]);

    }

}



dfsPrintPath(v);