Nesaistītās kopas
Nesaistītās kopas ir veids, kā realizēt priekšmetu sadalījumu vairākās kopās. No iepriekšējām nodaļām tika secināts, ka kopa ir kopums ar kaut ko. Vairākas kopas ir vairāki kopumi ar kaut ko, piemēram, 5 kopas, kur skaitļi dalās tikai ar 1, 2, 3, 4, 5 jeb katra skaitļa pakāpes. Nesaistītajās kopās eksistē 3 darbības, kuras strādā ļoti efektīvi (realizāciju skatīt 1. programmā):
- MakeSet(a) - izveido jaunu kopu a.
- Find(a) - katrai kopai ir nosaukums jeb par nosaukumu var kalpot kāda kopas elementa nosaukums, ja katrai kopai izvirza pārstāvošo elementu. Ar šo funkciju var atrast kopu pārstāvošā elementa nosaukumu.
- Union(a, b) - apvieno kopas a un b vienā.
MakeSet(a)
Parasti sākumā ir konkrēts elementu kopums, kas var glabāties masīvā. Katram elementam ir jābūt unikālam identifikatoram, par piemēru tiks apskatīta unikālu skaitļu virkne intervālā [0; 10]. Kopas realizācijai izmantotā struktūra skaitļu identifikatoru gadījumā var būt masīvs M, kur katru elementu jeb skaitli i raksturo šī masīva M[i] elements. Iepriekš tika apskatīts, ka koka struktūru var glabāt vecāku sarakstā jeb masīvā, kur masīva elementa indeks bija virsotnes numurs un elementa vērtība bija virsotnes vecāka numurs, citādi virsotne satur -1. M[i] tiek izmantots kā koka struktūra un sākotnēji nevienai kopai nav neviena vecāka, tādēļ MakeSet(a) piešķir M[i] = -1;.
Piemēram, sekojošās komandas realizēs 1. attēlā redzamo masīvu.
MakeSet pasaka, ka eksistē 1 kopa ar elementu a. Tātad tiek izveidotas 11 kopas,
kuru struktūra tiek realizēta masīvā M.
MakeSet(0);
MakeSet(1);
MakeSet(2);
MakeSet(3);
MakeSet(4);
MakeSet(5);
MakeSet(6);
MakeSet(7);
MakeSet(8);
MakeSet(9);
MakeSet(10);

Find(a)
Tika runāts, ka katrai kopai ir savs nosaukums vai pārstāvošais elements. Tā kā masīvs M ir koka struktūra, tad atzīmējot visus elementus ar -1, ir izveidojies mežs jeb vairāki koki, kur katrā ir viens elements. Kā ir zināms, tad kokam ir tikai viena sakne, tad šī sakne var arī būt kopas pārstāvošais elements. Sakni var atrast, ja elementam nav vecāks, jeb tas ir -1. Sākotnēji katrs elements atrodas savā kopā, kurai tas ir pārstāvošais elements. Ar Find(a) elementam a var atrast tā koka pārstāvošo element jeb sakni.
Union(a, b)
Divu kopu apvienošanai var izmantot divus elementus a un b. Algoritms, pēc kāda var apvienot divus elementus ir sekojošs:
- Atrod a kopas pārstāvošo elementu ar A = Find(a).
- Atrod b kopas pārstāvošo elementu ar B = Find(b).
- Ja A != B, tad M[B] = A. Ja iepriekš atrodot a un b kopas elementus A un B atšķīrās, tad tagad B vairs nav kopas pārstāvošais elements un Find(B) atgriezīs A, tādēļ tagad Fina(a) == Find(b) un a, b atrodas vienā kopā.
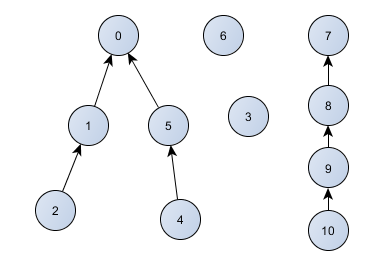
Piemēram, veicot sekojošas darbības, M struktūra izveidosies, kā 2. attēlā, kur var redzēt 4 kopas.
Union(0, 1);
Union(5, 4);
Union(0, 5);
Union(1, 2);
Union(7, 8);
Union(8, 9);
Union(9, 10);
Reitinga heiristika
Eksistē viena problēma ar līdz šim pārrunāto algoritmu. Piemēram:
Ir doti veseli skaitļi intervālā [0; 1000000]. Un tiek izsauktas komandas:
Union(0; 1);
Union(1; 2);
Union(2; 3);
...
Union(999998, 999999);
Union(999999, 1000000);
Piemērā izveidosies ļoti garš koks, kurš līdzināsies sarakstam. Problēma sāksies, ja mēģinās vairākas reizes izsaukt Find(1000000), jo Find nāksies iziet 1000000 virsotnēm cauri. Kopas raksturojošos kokus var balansēt izveidojot papildus masīvu R[], kur, ja i ir kopas elements, tad R[i] ir elementa apakškoka virsotņu skaits. Piemēram 2. attēlā R[0] == 5. Kā panākt, lai R tiktu aprēķināts pareizi? Ir nedaudz jāmaina divas darbības:
- MakeSet(a) - papildus ir jāpiešķir R[a] = 1, jo katrs elements no sākuma ir vienas virsotnes koks.
- Union(a, b) - nevis vienkārši piešķir M[B] = A, bet pārbauda, ja R[A] > R[B], tad M[B] = A un R[A] += R[B], citādi M[A] = B un R[B] += R[A].
Šīs darbības veicot, koks neveidosies lineārs, bet pletīsies platumā, līdz ar to koka dziļums būs ievērojami mazāks.
#include <iostream>
#define SIZE 11
using namespace std;
int M[SIZE];
int R[SIZE];
void MakeSet(int a)
{
M[a] = -1;
R[a] = 1;
}
int Find(int a)
{
if (M[a] == -1)
return a;
else
return Find(M[a]);
}
void Union(int a, int b)
{
int A = Find(a);
int B = Find(b);
if (A != B)
{
if (R[A] > R[B])
{
M[B] = A;
R[A] += R[B];
} else {
M[A] = B;
R[B] += R[A];
}
}
}
int main()
{
// Izveido kopas.
for (int i = 0; i < SIZE; ++i)
MakeSet(i);
// Apvieno kopas.
Union(0, 1);
Union(5, 4);
Union(0, 5);
Union(1, 2);
Union(7, 8);
Union(8, 9);
Union(9, 10);
// Izvada, kurās kopās atrodas elementi.
for (int i = 0; i < SIZE; ++i)
{
cout << "Elements " << i << " atrodas kopā " << Find(i) << endl;
}
return 0;
}








