Plaknē izvietoti N taisnstūri, kuru malas ir paralēlas koordinātu asīm. Taisnstūri var pārklāties, sakrist vai atrasties viens otra iekšpusē. Visu taisnstūru virsotņu koordinātas ir veseli nenegatīvi skaitļi un x koordināta nepārsniedz x_max un y koordināta nepārsniedz y_max. Ir novilkts nogrieznis AB, kura viens galapunkts atrodas punktā A(0, 0), bet otrs galapunkts B apmierina sekojošus nosacījumus:

• tā koordinātas ir veseli skaitļi;
• tas pieder vai nu nogrieznim [(0, y_max), (x_max, y _max)] , vai arī nogrieznim [(x_max, 0), (x_max, y_max)];

Nogrieznis AB var krustot taisnstūrus (uzskatām, ka krustošanās ir arī tad, ja nogrieznis šķērso vienu taisnstūra virsotni).

Uzrakstiet programmu, kas nosaka, kādu lielāko taisnstūru skaitu var krustot nogrieznis AB!

Ievaddatu pirmajā rindā dotas trīs naturālu skaitļu x_max, y_max (0< x_max, y_max ≤10⁹ ) un N (1≤N≤10000) vērtības. Katrā no nākošajām N rindām dots viena taisnstūra apraksts kā četru veselu skaitļu vērtības: apakšējā kreisā stūra koordinātas x_apkr un y_apkr un augšējā labā stūra koordinātas x_aula un y_aula . Starp katriem diviem blakus skaitļiem ir viens tukšumsimbols.

Izvaddatu vienīgajā rindā jāizvada viens vesels skaitlis - lielākais taisnstūru skaits, ko var šķērsot nogrieznis AB.

Pirmā piemēra testa zīmējums:

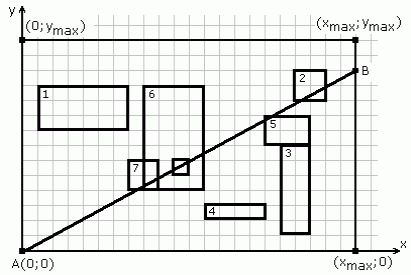
Punkts B var būt (22,11) vai (22,12).

 
Uzdevums izmantots Baltijas 10.informātikas olimpiādē Ventspilī 2004.gadā