Cipariem no 0 līdz n (1<=n<=9) ir definēta operācija @, kuras rezultāts arī ir cipars robežās no 0 līdz n. Piemēram, ja n=2, tad @ var aprakstīt ar sekojošas tabulas palīdzību, attēlojot visas iespējamās operācijas a@b vērtības (kur a un b - cipari robežās no 0 līdz 2):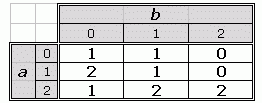

Kā redzams, šajā gadījumā operācija nav nedz komutatīva, jo 0@1 = 1, bet 1@0 = 2 , nedz asociatīva (0@1) @2 = 0, bet 0@ (1@2)=1.

Ja dota izteiksme x₁@x₂@x₃@x₄@...x_k-1@x_k (kur katrs x_i ir robežās no 0 līdz n), tad tās vērtību aprēķina no kreisās puses uz labo tāpat kā izteiksmes (...(((x₁@x₂)@x₃)@x₄)@...x_k-1)@x_k vērtību, sākot ar visdziļāk iekļautajām iekavām - vispirms aprēķina x₁@x₂ rezultātu r₁, pēc tam aprēķina r₁@x₃ rezultātu, utt. Mainot iekavu izvietojumu sākotnējā izteiksmē, tās rezultāts var mainīties.

Piemēram, ja dota izteiksme 1@1@1@1@0, tad piemērā redzamajai operācijai @ izteiksmes (1@ (1@1)) @ (1@0) vērtība ir 0, bet (((1@1) @1)@1) @0 vērtība ir 2.

Uzrakstiet programmu, kas dotam n, ar tabulu uzdotai operācijai @ un ciparu virknei x₁x₂x₃x₄...x_k-1x_k katram veselam skaitlim t (0<=t<=n) nosaka, vai izteiksmē x₁@x₂@x₃@x₄@...x_k-1@x_k iespējams salikt iekavas tā, lai šīs izteiksmes vērtība būtu t.

Ievaddatu pirmajā rindā dota naturāla skaitļa n vērtība (1<=n<=9). Nākošajā n+1 faila rindā ir uzdota operācija @. Katrā no šīm rindām ir n+1 cipars: faila i+2-ās rindas j+1-ais cipars ir operācijas i@j rezultāts (0<=i<=n,0<=j<=n). Starp katriem diviem blakus cipariem failā ir viens tukšumsimbols. Faila n+3-ajā rindā ir dota ciparu virkne x₁@x₂@x₃@x₄@...x_k-1@x_k bez atdalošiem tukšumiem. Virknes garums ir vismaz divi un ne vairāk kā 250 cipari.

Izvaddatiem jāsatur tieši n+1 rinda. Katram t (0<=t<=n) faila t+1-ajā rindā jābūt vārdam "VAR", ja iekavas dotajā izteiksmē iespējams salikt tā, lai izteiksmes vērtība būtu t, vai "NEVAR", ja šādi iekavas izvietot nav iespējams.

Uzdevums izmantots Latvijas 15.informātikas olimpiādes III (Valsts) kārtā. 

Autors: M.Opmanis